Table of Contents

Polynomial Formulas Class 10 Best pdf
Download this Class 10 Polynomial Formulas PDF for a comprehensive understanding of all essential concepts, identities, and theorems related to polynomials. This PDF is a perfect study resource for students preparing for their CBSE, ICSE, or state board exams. It covers:
- Standard Algebraic Identities: Learn the key identities like (a + b)², (a – b)², and others for easy expansion and factorization.
- Polynomials Types and Degrees: Understand the different types of polynomials such as linear, quadratic, and cubic, with examples.
- Zeroes and Factors: Get step-by-step instructions on how to find the zeroes of polynomials and their corresponding factors.
- Important Theorems: Master the Factor Theorem, Remainder Theorem, and Division Algorithm for solving polynomial problems.
Standard Algebraic Identities

Standard Algebraic Identities
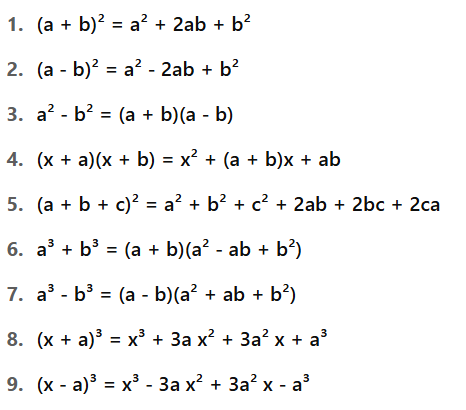
hese identities are used in:
- Expanding algebraic expressions
- Simplifying expressions
- Factorizing polynomials
- Polynomial Formulas Class 10 Best pdf
Polynomials: Types and Degrees

. Types of Polynomials
Polynomials are classified based on the number of terms they contain. The types are:
a) Monomial
- A polynomial with only one term.
- Example: 3x, 5, -7xy
b) Binomial
- A polynomial with two terms.
- Example: x + 2, a – b, 3x² + 5x
c) Trinomial
- A polynomial with three terms.
- Example: x² + 3x + 2, a² + 2ab + b²
d) Multinomial
- A polynomial with more than three terms.
- Example: x³ + 3x² + 5x + 7
2. Degree of a Polynomial
The degree of a polynomial is the highest power of the variable (or the sum of the powers of the variables in case of more than one variable).
a) Degree of Monomial
- The degree of a monomial is the exponent of its variable.
- Example: 3x² has a degree of 2.
b) Degree of a Binomial
- The degree of a binomial is the highest degree of any term in the binomial.
- Example: x + 2 has a degree of 1 (degree of x).
- Example: 3x² + 2x has a degree of 2 (degree of x2).
c) Degree of a Trinomial
- Similar to binomials, the degree of a trinomial is the highest degree of any term.
- Example: x² + 3x + 2 has a degree of 2 (degree of x2x^2×2).
- Example: a³ + b² + c has a degree of 3 (degree of a3a^3a3).
d) Degree of Multinomial
- The degree of a multinomial is determined by the term with the highest degree.
- Example: x³ + 3x² + 5x + 7 has a degree of 3 (degree of x3).
- Example: 2x²y + 3xy² + 5xy has a degree of 3 (degree of xy²).
Degree of a Polynomial – Key Points:
- Zero Polynomial: A polynomial that is equal to 0. Its degree is considered undefined or sometimes said to be negative infinity.
- Constant Polynomial: A polynomial that has no variable (e.g., 5). Its degree is 0 because there’s no variable.
Summary of Polynomial Types and Degrees

Zeroes of a Polynomial

The zeroes (or roots) of a polynomial are the values of the variable that make the polynomial equal to zero. In other words, if p(x) is a polynomial, the zeroes are the values of x for which p(x) = 0.

How to Find the Zeroes ?
Method 1: Factorization Method (for Quadratic Polynomials)
Factorize the polynomial and solve for x. This works well for polynomials that can be factored easily.
- Factor the polynomial into two binomials (if possible).
- Set each factor equal to 0.
- Solve for x.

Method 2: Quadratic Formula (when factorization is difficult)
The quadratic formula is used for finding the zeroes of any quadratic polynomial of the form ax² + bx + c = 0.
The quadratic formula is:

Where:
- a, b, and c are the coefficients of the quadratic polynomial ax² + bx + c.
Example 2:
Find the zeroes of p(x) = 2x² – 4x – 6.
- Identify the coefficients:
a = 2, b = -4, c = -6 - Apply the quadratic formula:

3. Corresponding Factors of a Polynomial
Once you find the zeroes, you can easily express the polynomial in its factored form using the zeroes.
If the zeroes of a polynomial are x = α and x = β, the polynomial can be written as: p(x)=a(x−α)(x−β)p(x) = a(x – α)(x – β)p(x)=a(x−α)(x−β)
Where a is the leading coefficient (if the polynomial is not monic).
Example:
For the polynomial p(x) = x² – 5x + 6, we found the zeroes x = 2 and x = 3. Therefore, the factorized form of the polynomial is: p(x)=(x−2)(x−3)p(x) = (x – 2)(x – 3)p(x)=(x−2)(x−3)
4. Important Notes
- If p(x) is a monic polynomial (leading coefficient = 1), the factors are easier to find directly using zeroes.
- For higher-degree polynomials (degree 3 or more), the process is similar, but you may need synthetic division or more advanced factorization methods.
Summary:
- Zeroes of a polynomial are the values of x that make the polynomial equal to zero.
- Factorization is the most common method for finding zeroes, but the quadratic formula can be used when the polynomial is not easily factorable.
- Once zeroes are found, you can write the polynomial as a product of its factors.
Important Theorems in Class 10 Polynomials

1. Remainder Theorem
Statement:
If a polynomial p(x) is divided by (x – a), then the remainder is p(a).
🔹 Use:
Quickly find the remainder without actual long division.
🔹 Example:
Let p(x) = x³ + 2x² – 3x + 1
Divide by (x – 2).
Then, remainder = p(2)
p(2)=(2)3+2(2)2−3(2)+1=8+8−6+1=11
Remainder = 11
2. Factor Theorem
Statement:
If p(a) = 0, then (x – a) is a factor of p(x).
Also, if (x – a) is a factor of p(x), then p(a) = 0.
🔹 Use:
To check if a given binomial is a factor of a polynomial.
🔹 Example:
Let p(x) = x² – 5x + 6
Check whether (x – 2) is a factor. p(2)=(2)2−5(2)+6=4−10+6=0
✅ Since p(2) = 0, (x – 2) is a factor.
3. Division Algorithm for Polynomials
Statement:
If p(x) and g(x) are two polynomials with g(x) ≠ 0,
then there exist polynomials q(x) and r(x) such that

Where:
- p(x) = dividend
- g(x) = divisor
- q(x) = quotient
- r(x) = remainder, and either r(x) = 0 or degree of r(x) < degree of g(x)
🔹 Use:
To divide one polynomial by another and express it in terms of quotient and remainder.
🔹 Example:
Divide p(x) = x³ – 3x² + 5x – 3 by g(x) = x – 1
By long division, we get:
- Quotient: x² – 2x + 3
- Remainder: 0
When to Use Which Theorem
| Theorem | Purpose |
|---|---|
| Remainder Theorem | To quickly find the remainder of division by (x – a) |
| Factor Theorem | To check if (x – a) is a factor of a polynomial |
| Division Algorithm | To divide one polynomial by another and express in quotient-remainder form |
